Classical theories of gravity produce entanglement

To illustrate this further, we now demonstrate how equation (4) leads to entanglement in a version of Feynman’s experiment. Two spherical mass distributions, each with a total mass Mr. and radius A.are prepared in a quantum superposition of two locations. This could be achieved, for example, by implementing matter wave beam splitters.⁶manipulate potentials³² or by exploiting internal degrees of freedom, such as quantum spins in Stern-Gerlach experiments⁵ (Fig. 3). Gravity is assumed to be the only interaction between particles, and in the non-relativistic limit and describing matter in the first quantification, it simply acts as a quantum phase. φ_Ij ≔ GMr.²t/(ħ d_Ij) on each overlay branch^5.6Or d_Ij is the distance between the matter distributions in the branch labeled by I, j ∈ {L, R} and GMr.²/d_Ij is the Newtonian potential energy. With overlay size Δx much greater than the smallest distance d_R.L.only the quantum phase φ ≔ φ_R.L. is significant, so that the systems are clearly entangled, the entanglement depending only on φ (ref. ^5.6). On the other hand, when Δx ≪ d_R.L.the relevant parameter for entanglement essentially becomes \(\overline{\varphi }:= \varphi \,\Delta {x}^{2}/{d}_{{\rm{RL}}}^{2}\)(ref. ³³). To measure entanglement, the overlapping paths could be recombined and correlations sought between the interferometer outputs.⁶ or internal degrees of freedom⁵.

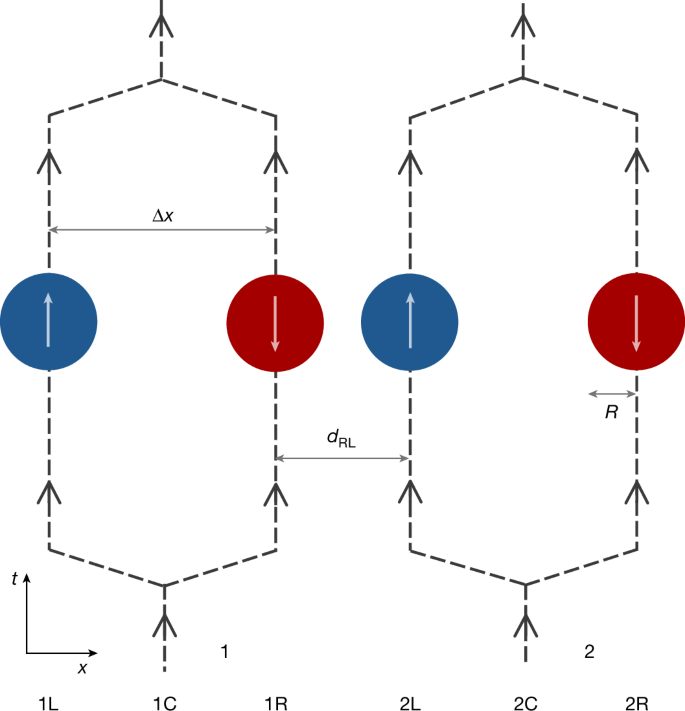
Two spherical mass distributions (1 and 2) of radius A. are placed in quantum superpositions in two places as N00N states, with blue and red denoting components separated by Δx. After a short period of gravitational interaction, the paths are recombined and entanglement is searched.^5.6. Although Stern–Gerlach interferometry with internal spins is shown⁵alternative configurations, such as parallel Mach–Zehnders, are also possible⁶. Here, Δx is shown larger than the minimum separation d_R.L.but a general configuration can be implemented, including Δx ≪ d_R.L..

Quantum gravity

We now analyze this experiment using perturbative quantum gravity with a QFT description of matter. Ignoring electromagnetic interactions, we take the initial state of objects immediately after being placed in a quantum superposition as a product of N00N states:

where |N⟩_κI is a product of N independent position states of matter particles obeying a complex scalar field³⁴with κ ∈{1, 2} and I ∈ {L, R} labeling the position of spherical objects (corresponding to Fig. 3). N is the number of particles in objects, such that Mr.= mN with mthe mass of the particles. We also include possible internal spin states {|↑⟩ |↓⟩}, which could be used to generate quantum superpositions.

After a while t the state of the matter system in Schrödinger’s image is

Or \(\broad hat{T}\)is the time scheduling operator, τis a dummy time variable, \({\wide hat{H}}_{0}\)is the Hamiltonian of perturbative quantum gravity in the absence of matter-gravity interactions and \({\widehat{H}}_{{\rm{I}}} := \exp ({\rm{i}}{\widehat{H}}_{0}t/\hbar ){\widehat{H}}_{{\rm{int}}}\,\exp (-{\rm{i}}{\widehat{H}}_{0}t/\hbar )\). Just before the superposition paths are bought together, e.g. via reversed Stern–Gerlachs^1.5we can write

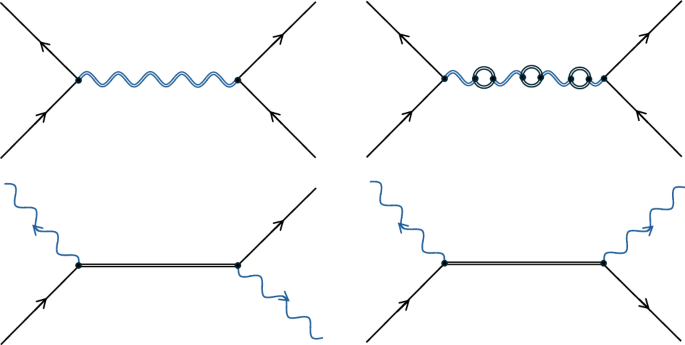
Or \({\alpha }_{ij}\in {\mathbb{C}}\) . We have now neglected internal spin states and vacuum states for simplicity. We can calculate the amplitudesα_Ij by taking the dot product of equation (7) (and also equation (6)), with the basis states |N⟩_1I|N⟩_{2 j} and extending the time-ordered unit operation in equation (6) in the form of the Dyson series^26.35. The amplitudes can then be written in the form of a perturbative series, each term of which corresponds to that of the Dyson series: \({\alpha }_{ij}={\alpha }_{ij}^{(0)}+{\alpha }_{ij}^{(1)}+{\alpha }_{ij}^{(2)}+\cdots \,\) . The first process in which a virtual graviton is exchanged between matter objects occurs at the second order of the series and corresponds to the Feynman diagram in Figure 1 (top left). The amplitude of this Feynman diagram, in the very good approximationct ≫  d_Ij (Methods), is

Orθ_κI(x)≔ θ ( A.−∣x− X_κI∣ ) is the unitary function defining the spherical shape of the matter distribution κin branch I,X_κI is the coordinate of the center of mass for the distributions andV  ≔ 4πA.³/3. The above amplitude directly contributes to \({\alpha }_{ij}^{(2)}\)such that, when Δx ≫ d_R.L.THE \({\alpha }_{{\rm{RL}}}^{(2)}\) the amplitude dominates all others and is equal to i φ. So, given that \({\alpha }_{ij}^{(0)}=1\)from the Dyson series and that \({\alpha }_{ij}^{(1)}\) does not contain any contraction for the gravitational field, we are left α_Ij≈ 1 except forα_R.L.≈ 1 + I φwhich maps the first quantized result to first order in the quantum phase \(\exp ({\rm{i}}\varphi )\) . The complete non-perturbative result is obtained simply by considering the shape of the corresponding higher-order Feynman diagrams and extrapolating the result.²⁶.

Classic Gravity

We now consider the above experiment in the context of classical gravity. The calculation follows the above but with the Hamiltonian interaction of equation (4) rather than equation (2). At second order in the Dyson series, there are no nonzero Wick contractions corresponding to Feynman diagrams that contain quantum communication between matter objects, and the diagram responsible for entanglement in quantum gravity, Figure 1 (top left), becomes Figure 2 (top middle). This diagram depicts the two matter objects sitting in their combined classical gravitational field, with the amplitude simply contributing to a local relative quantum phase between the branches of each matter object, which does not lead to entanglement.¹³. However, at the fourth order of the series, a diagram appears in which the matter distributions are quantum-mechanically connected via virtual matter particles (Fig. 2, top right). In the same approximations as in the case of quantum gravity, the amplitude of the Feynman diagram is (Methods)

OrΦ(x) ≔− c²h⁰⁰(x)/2 is the total gravitational potential of matter objects, and ϑ_Ij directly contributes to \({\alpha }_{ij}^{(4)}\) in equation (7). Since we have a classical theory of gravity, Φ(x) is the same in each superposition branch, otherwise the Newtonian force would be in a quantum superposition. Some work has considered gravity to be classical but nevertheless allows the Newtonian field or force to be in a quantum superposition^36,37,38,39. Here we stick to the idea that quantum superposition is a purely quantum phenomenon such that Φ(x) is not superimposed in equation (9) and is not a quantum operator. However, despite this, equation (9) generally results in entanglement, asθ_{1 I}(x) Andθ_{2 I}(x) are different for different overlay paths and are connected via∣x−Yes∣such as \({\alpha }_{ij}^{(4)}\)is different for each overlay path, except for \({\alpha }_{{\rm{LL}}}^{(4)}={\alpha }_{{\rm{RR}}}^{(4)}\)symmetry. We can understand this from the Feynman diagram in Figure 2 (top right), where, unlike the gravitational potential, the virtual matter particles enter into a quantum superposition with the different mass states and the distance the virtual matter particles propagate is different in each branch, making the space integrals of equation (9) connected via ∣x−Yes∣.

As Φ (x) arises from a superposition of matter in equation (9), we need to consider exactly how gravity arises from quantum matter in a fundamental theory of classical gravity. In the most considered approach^40.41, Φ(x) in equation (9) is the sum of the average potentials of the superposition states of the two objects. In this case, ϑ_Ij is inversely proportional tod_Ij such that, if Δx ≫ d_R.L. the RL amplitude dominates all others and is∣ϑ_R.L.∣≈ ϑwhere (Methods)

The state in equation (7) is then clearly entangled, because, just as in quantum gravity, α_R.L.contains a contribution ϑit is not in any of the other amplitudes α_Ij. Moreover, like quantum gravity³³inverse scaling of ϑ_Ij withd_Ij allow \(\overline{{\vartheta }}:= {\vartheta }\,\Delta {x}^{2}/{d}_{{\rm{RL}}}^{2}\)be identified as the relevant parameter for entanglement when Δx ≪ d_R.L..